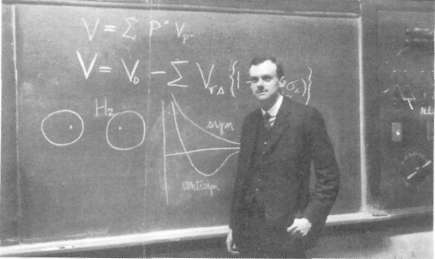|
|
|
|
|
|
|
|
|
|
İR fizik kuramı, matematiksel güzelliğe sahip ol
|
|
|
|
|
malıdır." Bu, 1976'da kendisine fiziğin ne olduğu sorulduğunda Paul Dirac'ın verdiği yanıttı. Dirac, kuramsal fizik alanındaki saygın kariyeri boyunca çoğu zaman fiziğin estetik ve mantıksal yönlerini vurguladı. Bu yaklaşım ona bazen inanılmaz ilerlemeler sağlamakla birlikte, onu sıklıkla verimsiz yan yollara da yöneltti.
Gençliğinde bile bir deha ve özgür düşünür olarak tanınan Dirac'ın fiziği ele alış biçimi yenilikçi, ama anlaşılması da bir o kadar güçtü. 1926'da Eins-tein, o zaman 24 yaşında olan bu Cambridge fizikçisinin bir makalesini anlamaya çalışırken şöyle demişti: "Di-rac ile başım dertte. Dehayla deliliğin, bu başdöndürücü zikzak yolda dengelenmiş olması, berbat bir şey!".
Şimdi? doğumundan yüz yıl sonra, Dirac'ın dünyanın yeni bir dünya tab-losuyla sonuçlanan bilimsel devrimdeki benzersiz rolü artık tam olarak anlaşılıyor. İtalyan fizikçi Antonino Zic-hichi'nin yakın zamanda söylediği gibi, Dirac'ın çağdaş fizik üzerindeki etkisi, Einstein'ınkinden bile daha büyük olmuş olabilir.
Yaşamı ve Çalışmaları
Paul Adrien Maurice Dirac, 8 Ağustos 1902'de Bristol'da (İngiltere) doğdu. Babası İsviçre'de Fransızca konuşan bir kantondan olan Dirac, 1919'da İngiliz vatandaşlığına girinceye kadar İsviçre vatandaşı olarak büyüdü. Bristol Üniversitesi'nde elektrik mühendisliği ve uygulamalı matematik okuduktan sonra Ralph Fowler'in gözetiminde araştırma Öğrencisi olarak Cambridge Üniversitesi'ne girdi. 1925 sonbaharında da kuantum mekaniğinin kendi versiyonu olan ve "q-sayısı cebiri" olarak bilinen çalışmasıyla kuramsal fizikte büyük bir atılım yaptı.
Daha sonraki birkaç yıl içinde Dirac yeni "kuantum fiziği"nin lideri durumuna geldi. En yaratıcı dönemiyse, günümüz kuantum mekaniğinde temel önemi olan yepyeni kuramlar geliştirdiği 1925-1933 arası dönemdir. Örneğin 1927'de şimdi Fermi-Dirac istatistiği denen kuramı bağımsız olarak geliştirdi ve kuantum elektrodinamiği konusunda öncülük eden bir makale yazdı: "Işınım yayımı ve soğurulmağının
|
|
|
|
FİZİKTE GÜZELLİK ARAYIŞI
PAUL DİRAC
|
|
|
|
kuantum kuramı". Ertesi yıl da elektronlar için relativistik dalga denklemini geliştirdi ve onu kullanarak, daha Önce yalnızca bir doğa olayı olarak algılanan "spin" (dönme) ve manyetik moment kavramlarını açıkladı. Daha da önemlisi, bu kuramın 1934'te Dirac'ın karşı-elektron ve genel olarak karşı-parçacıkların varlığını Öngörmesine yol açan fikirlerinin başlangıç noktası olması.
Dirac'ın 1930'da, 27 gibi oldukça genç bir yaşta Royal Society'ye üye seçilmesi, onun bilimsel saygınlığının bir göstergesidir. O sırada Manchester Üniversitesi'nde bir kürsü teklifi almış ve onu geri çevirmişti. 1932'de, Camb-ridge'de bir zamanlar Isaac New-ton'un, günümüzdeyse Stephen Haw-king'in getirildiği "Lucasian" kürsüsü matematik profesörlüğüne atandı.
Dirac'ın yaşamındaki bir başka önemli olay, 1933 yılında "atom kuramı ve uygulamaları için yeni verimli biçimlerin keşfi" ile Nobel Fizik ödü-lü'nü Erwin Schrödinger ile paylaşma-
|
sıydı. Emekli olduğu 1969 yılına kadar Lucasian profesörlüğünü sürdürdü; sonra, Tallahassee'deki Florida Eyalet Üniversitesi'nin fizik bölümüne katıldı. ABD'de kaldığı süre boyunca Dirac üretkenliğini sürdürdü ve 20 Ekim 1984'teki ölümünden kısa bir süre öncesine kadar, fizik araştırmalarına devam etti.
Sembolik Yöntem
Dirac Bristol'da mühendislik Öğren-cisiyken bazı felsefe kitapları okumuş, ancak daha sonra anımsadığına göre, felsefenin yararını anlama çabalan başarısız olmuştu: "Sonunda felsefenin fiziğe herhangi bir katkıda bulunamayacağına karar verdim." Dirac felsefeyi ciddiye almıyordu. Bir keresinde onu "zaten gerçekleşmiş keşifler hakkında bir konuşma ve yorum yapma biçimi" olarak tanımlamıştı. Ne var ki, bilim felsefecilerinin kullandıkları bazı düşünce kalıpları, onun fiziğe yaklaşımının da belirleyici niteliğiydi.
|
|
|
|
|
|
|
|
BİLİM ve TEKNİK 84 Ocak 2004
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Genel olarak "doğrulamacılığın" (pozitivizm) özelliklerini desteklerdi. Fiziğin yalnızca, deneysel olarak sınanabilir öngörüler yapmak için bir araç olduğu ve bir fizik kuramının, İlke olarak gözlemlenebilir niteliklerden oluşması gerektiğini savunan "araçsalcılık" (enstrümantalizm) gibi. Dirac, Heisen-berg'in 1925'te öne sürdüğü kuantum mekaniği kuramının temelini oluşturan bu öğretiyi, yine onun aracılığıyla benimsemişti. Ancak bu Öğretiye her zaman bağlı kalmadı ve gözlemlenebilir sayılamayacak nicelikler önerdiği de oldu. Gözlemlenebilir olmayan şeylerin de fizik kuramlarından tümüyle dışlanamayacağını farketmişti. Nedeni, gözlemlediklerimizin yalnızca doğadan gelmemesi, kısmen de doğayı anlamak İçin kullandığımız kuramlarla saptanmış olmasıydı.
Fiziğin amacı, Dirac'a göre, dünyanın özelliklerini ortaya koymak değil, yalnızca deneysel sonuçları hesaplama yöntemlerini sağlayacak somut sistemler oluşturmaktı. Anlam, yorum ve ontoloji, yani dünyada neyin gerçekten varolduğu sorulan tümüyle yersizdi. 1936'da Max Born, Dirac'ın yaklaşımını şöyle ifade etmişti: "Bütün İstediğimiz, matematik açısından tutarlı bir kuramdır. Deneysel dünya hakkında söylenebilecek her şeyi o temsil eder. Onun yardımıyla, gözlemlenmemiş olayları öngörebiliriz ve İstediğimiz de bundan ibaret. Nesnel dünya İle ne kastettiğinizi bilmiyoruz ve önemsemiyoruz."
Dirac doğrulamacı erdemlere övgüsünü sürdürürken, İkinci Dünya Sava-şı'ndan sonra, bir fizik kuramı için öngörme yetisinin yeterli olmadığını da sıkça vurgulayarak, bilimsel anlayışın aynı zamanda güzellik ve yalınlık gibi ölçütleri de sağlaması gerektiği görüşüne daha fazla yöneldi; bunlar öngörme ölçütüyle uyuşmasa bile.
Dirac'ın matematiksel yöntemleri, özellikle de olayları öngörmek için kullanılabilecek denklemleri yeğlediği ortadaydı. Kuantum mekaniğinin yorumlanması gibi felsefi önemi olan daha kapsamlı sorular ilgisini çekmedi. 1927'deki Solvay toplantısına katıldı ve Einstein ile Niels Bohr arasındaki ünlü tartışmayı izledi. Kuramsal fiziğin bu iki devinin tartıştığı konu, kuantum mekaniğinin eksiksiz bir kuram olup olmadığıydı. Daha sonra Dirac "Onları
|
|
|
|
|
dinledim ama tartışmaya girmedim; Çünkü aslında konuyla pek o kadar da ilgilenmiyordum. Beni asıl ilgilendiren, doğru denklemleri elde etmekti" demişti.
Benzer şekilde, Bohr'un kuantum mekanik anlayışıyla hemfikir olduğu halde, onun kuantum dünyasının Kopenhag yorumunun temel taşlarından biri olan "tümleyicilik (complementarity) ilkesinden hiç hoşlanmamıştı. ' Bohr'un İlkesine göre, elektron gibi fiziksel nesneler yalnızca parçacık ve dalga gibi birbirini dışlayan kavramlar tarafından tam olarak İfade edilebilirdi. Dirac'ın bundan hoşnut olmama nedeni, tümleyicilik ilkesinin "daha önce sahip olmadığımız denklemlere yol açmıyor" olmasıydı.
Araçsalcılık eğiliminden beklenebileceği gibi, Dirac'ın kuantum mekaniğine cebirsel yaklaşımı son derece soyuttu ve deneylere ya da sayısal verilere pek az atıfta bulunuyordu. 1930'da yazdığı "Kuantum Mekaniğinin İlkeleri" isimli ünlü ders kitabı, "sembolik yöntem" adını verdiği yönteme dayalıydı. Bu yöntem "temel önem taşıyan nicelikleri doğrudan soyut biçimde ele alıyor...ve nesnelerin doğası konusuna daha derinden yaklaşıyordu". Dirac, kuantum mekaniğinin genel kuramını fiziksel yorumdan bağımsız olacak bir yolla ifade etmek istiyordu: "Kullanılan sembollerin hiçbir yerde kesin biçimde belirlenmediği, ya da bunun hiç gerekli olmadığı bir yolla. Onlar hep soyut bir biçimde kullanılıyorlar; İstenen yalnızca sağladıkları cebirsel aksiyomlar, ve onları içeren denklemlerle fiziksel koşullar arasındaki bağlantı."
Sembolik yöntem bazı fizikçileri korkutmuş, ama başka bazılarının da ilgisini çekmişti. Örneğin İngiliz gökbilimci Arthur Eddington, Dirac'ın fizik yönteminden büyülenmişti. Onu "son derece fızikötesi, neredeyse mistik" olarak övmüş ve kendisinin maddesel-
|
likten arınmış, matematik sembolleriy-le donanmış bir gölgeler dünyası şeklindeki evren görüşüyle çok uyumlu bulmuştu.
|
|
|
|
|
|
|
|
Dirac'ın matematiğin gücü konusunu vurgulamasının ontolojik (var olmayla ilgili) sonuçlan da oldu. Görüş-lerini hiçbir zaman, âçıkça_ifade-etme-di; ancak bazı durumlarda, bazı_ fiziksel niceliklerin varlığını doğrudan matematik kuramlarını kullanarak sapta-dı. Temel kuramlarda ortaya çıkan birçok matematiksel niceliğin doğada bir karşılığı olduğuna -yani fiziksel bir varlığa sahip olduğuna- inanma eğilimi vardı. Başka deyişle, matematiksel bakımdan tutarlı olan betimlemelere sa-
|
|
|
|
hip olan -ve temel fizik Tasalarının olanaksız kılmadığı- her varlığın doğada da var olması gerektiğini kabul edİyor-
|
|
|
|
Dirac'ın bu görüşü, "bolluk İlkesi (principle of plenitude)" olarak bilinen eski bir metafizik öğretisinin çağdaş versiyonudur, özellikle Newton'un çağdaşı Gottfried Leibniz'in benimsediği bu ilkeye göre, olanaklı olduğu düşünülen her şeyin aynı zamanda fiziksel gerçekliğe de sahip olması gerekiyordu. Bu İlke, Örneğin, 17. yüzyılda denizkızlarının görüldüğü iddiasını, daha sonra da bilinmeyen bitkiler, dünya-dışı yaratıklar, ve yeni kimyasal elementlerin varlığını desteklemek için kullanılmıştı. Dirac da bu bolluk ilkesinden sıkça yararlandı. En çarpıcı örneklerden biriyse, karşı-elektron ile manyetik tek-kutbu (monopole) ortaya koyduğu ilginç 1931 makalesidir.
Dirac, bu makalenin yöntemsel giriş bölümünde kuramsal fiziğin ilerlemesi İçin bir krallar yolu önerdi. İlerlemeye giden yolun "kuramsal fiziğin temelini oluşturan matematiksel biçimselliği kusursuzluğa ve genelliğe ulaştıracak
|
|
|
|
|
|
|
|
Ocak 2004 85 BİLİM veTEKNİK
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dirac'ın genel felsefesi, fiziksel durumun çözümü için matematiğe güvenmek ve önceliği fiziksel deneyselliğe değil, matematiksel biçimselliğe vermek şeklindeydi. Elbette kastettiği, temel fiziğin bütün matematiksel sonuçlarının bir fiziksel gerçekle eşleştiği değildi. Bolluk ilkesini kullanımı, onun kısa sürede düşüncelerinin merkezine yerleşecek olan "güzel matematik" anlayışına dayanıyordu.
Matematiksel Güzellik
İleri matematiğe olan tutkusuna karşın, Dirac basit olan ve fizik problemlerinin çözümünde doğrudan kullanılabilen matematik kavramları yeğlerdi. Önemli olan, kesin denklemler, katı İspatlar ya da aksiyom sistemleri değil, doğru matematiksel sezgi ve uygun araçlardı.
Dirac'ın matematiksel titizliği fazla Önemsememesi, belki de daha Önce gördüğü mühendislik eğitiminde yaklaşık yöntemlerin ve yüzeysel matematiğin değerini kavramış olmasından kaynaklanıyor olabilir. Relativistik dalga denklemini elde ederken kullandığı şaşırtıcı yöntem fizikçileri çok etkilemişti; ama matematiksel temeli pek güçlü sayılmazdı. Denklemde görülen 4x4 matrislere, uygulamada kullanılması olası ve uygun nicelikler olarak bakıyordu; ancak onların matematiksel niteliklerini saptamayı pür matematikçilere bırakmıştı. "Spinor analiz" denen matematik dalı bunun sonucudur.
Dirac'ın, Kuantum Mekaniğinin İlkeleri kitabının Önsözünde "matematik bir araçtır" görüşünü vurgulamasına karşın, matematiğe bakışının bir başka yönü de vardı. 1935 yılından başlayarak matematik için güçlü bir estetik görüş geliştirmeye başladı: doğa yasalarının belirleyici niteliği, yüksek düzeyde matematiksel "güzellik"ti. Güzel matematik denklemleriyle fiziksel dünyanın İşleyişi arasında derin bir uyum vardı.
1939'da bir yazısında "matematikçilerin ilginç buldukları kuralların doğanın da seçimi olduğu, zamanla daha da belirginleşiyor" diyordu. Daha sonra 1963'te, Tanrı'yı şöyle betimliyordu: "Evreni yapılandırırken çok ileri matematik kullanan, çok yüksek düzeyde bir matematikçi".
|
|
|
|
Dirac (solda), Richard Feynman'la 1962'de Polonya'da gerçekleşen "Relativistik Kütleçekim Kuramları Uluslararası Konferansı" sırasında tartışırken. Dirac, bir kuramın "güzel" ya da "çirkin" olduğunu sezgisel olarak bilirdi. Çirkin matematik için verdiği başlıca örnekse Feynman ve başka fizikçiler tarafından geliştirilen kuan-
tum elektrodinamik kuramıdır. Ona göre bu kuram gereksiz ölçüde karmaşıktı ve sağlam olmayan matematiksel akıl yürütmelere dayanıyordu. Her ne kadar deneylerle uyumlu olsa da, Dirac kuramın temelde
doğru olmayacağı kanısındaydı.
|
|
|
|
girişimlerde, pür matematiğin bütün kaynaklarını kullanmak ve bu yöndeki her başarıdan sonra yeni matematiksel özellikleri fiziksel varlıklarla yorumlamaya çalışmak" olduğuna inanıyordu.
Bu yöntemle Dirac kuantum mekaniğini kullanarak manyetik yüklerin, yani monopollerin, tutarlı biçimde açıklanabileceğini kanıtladı. Onun manyetik monopolü, yalnızca kuantum kuramı uyannca varolan varsayımsal bir parçacıktı; ama Dirac, potansiyel varolmayla gerçek varolmanın aynı şey olduğuna inanıyordu. Monopoller, engelleyici kuramsal gerekçeler yoksa doğada bir yerlerde neden var olmasınlardı? Ya da, kendi ifadesiyle "doğanın onları biç kullanmaması şaşırtıcı olmaz mıydı?"
1960'larda fizikçilerin bu gizemli parçacığı ciddi biçimde aramaya başlamalarında, bu tür bir bolluk gerekçesi önemli rol oynadı. Ne var ki, yıllar süren başarısız deneyler (ve bazı saptama iddiaları) bolluk gerekçesine güveni zorlaştırdı. 1976'da Dirac problemin yalnızca deneysel olarak saptanabileceği sonucuna vardı. Monopollerin belki de varolmadığını ise, 1981'de ünlü fizikçi Abdus Salam'a bir mektubunda dile getirdi.
Dirac, monopolü öngördüğü sıralarda, 1928'de elde ettiği relativistik dalga denkleminin negatif-enerjİ çözümü-
|
nü yorumlarken de benzer yöntemler kullandı. Parçacıklar negatif enerji ta-şryamadıkları halde Dirac, kuramda ortaya çıkan negatif enerji durumlarının fiziksel birşeyleri temsil ettiği konusunda ısrarlıydı. Bu nedenle de 1930'da negatif enerji sürekliliğinde "deliklerin varlığını içeren ünlü bir yorum öne sürdü ve bu deliklerin protonlar olabileceğini söyledi. Ertesi yıl da deliklerin varsayımsal "karşı-elekt-ron"lar -pozitif yüklü elektronlar- olduklarını ileri sürdü. Ancak, delikler gerçekten karşı-elektronlardan oluşuyorsa, öteki elektronlarla yok olarak gama ışınları oluşturabilirlerdi. Böyle bir şey doğada gerçekleşebilir miydi? Dirac'a göre yanıt "evet" idi. "Bu tür süreçlerin dünyada bir yerlerde olmaması için bir neden yok. Bunlar bütün genel doğa yasalarıyla tutarlı olurdu" diye yazmıştı. Protonların kılık değiştirmiş elektronlar oldukları yolundaki kısa ömürlü varsayım, tam da Dirac'ın hoşlanacağı türdendi. Çünkü felsefecilerin hayal ettiği şeyi gerçekleştirmeyi vaadediyor ve bütün maddeyi tek bir parçacığın, yani elektronun farklı görünümlerine indirgiyordu. Dirac, kura-mındaki deliklerin gerçekten anti-elektronlar olmalarına karşın, bunların protonlardan çok farklı parçacıklar olduğunu sonunda anladı. Doğa onun sandığı kadar yalın değildi.
|
|
|
|
|
|
|
|
BİLİM ve TEKNİK 86 Ocak 2004
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Matematikle fizik arasında önceden kurulu bir uyum olduğu düşüncesi yeni değildir; Dirac'ın yaptığıysa, doğanın temel yasaları konusunda bilgi elde etmenin yolunun, güzel matematikten geçtiğini vurgulaması. Ama güzel matematik nedir? Dirac bu kavramı tanımlamadı; buna gerek de olmadığını düşündü. "Matematiksel güzellik, sanattaki güzellikte olduğu gibi, tanımlanamayan bir gü
|
|
zelliğin bazı durumlarda deneylere uyumdan öncelikli olduğuna ve bu nedenle bir doğruluk ölçütü yerine geçeceğine inanıyordu. Matematiksel olarak çirkin bir kuram, doğru olamazdı.
Her ne kadar Dirac güzellik ve çirkinliği tanımlayama-sa da, bir kuramın bu iki sınıftan hangisinde olduğunu sezgisel olarak bildiğine inanıyordu. Matematiksel olarak "çirkin" bir kuram için verdi
|
|
|
|
|
|
|
|
|
ği birincil örnek, Richard
|
|
|
|
zelliktir; ama matematikle
|
Dirac, ünlü atom fizikçileri Niels Bohr (solda) ve Werner Heisenberg (ortada) ile.
|
|
|
|
|
|
|
|
uğraşan insanlar onu farket-mekte zorlanmazlar."
Gerçekliği güzellikle saptama fikri, Dirac'ın deneysel-tümevarımsal yöntem yerine tek yönlü matematiksel-es-tetik yöntemi vurgulamasına yol açtı. Dirac daha sonraki yaşamında, matematiksel güzellik gibi belirsizliği bariz
Büyük Sayılar
|
olan bir kavramı, her zaman deneysel sınamadan üstün tuttu. Hatta deneylerin, Einstein'ın genel görelilik kuramı gibi matematiksel açıdan güzel olan bir kuram için ters sonuçlar vermesi durumunda, yanlış olanın deneyler olduğunda ısrarlıydı! Matematiksel gü-
|
Feynman ve başka bazı fizikçilerin kuantum elektrodinamiği kuramlarıydı. Kuramın karmaşık ve belirsiz olduğu kadar, sonsuz nicelikleri dışlamak da dahil, sağlam olmayan matematiksel argümanlara dayandığını söyledi. Her ne kadar çok iyi sonuçlar veriyor ve deneylerle son derece uyumluysa da kuram, Dirac'a göre temelde doğru olamazdı.
Dirac'ın bir araştırma aracı olarak matematiksel güzelliğin gücüne olan inancının, bilimin geçmişindeki örnekleri oldukça sınırlı. Kendi kariyerinin de, inancının tersini izlemesi İlginçtir. Dirac hemen hemen bütün büyük keşiflerini 1925 ile 1933 arasında yapmıştı. Matematiksel güzellik düşüncesinin egemen olduğu 1935'ten sonra, daha önce yaptıklarıyla kıyaslanabilir değerde fizik üretmedi.
Gerçekte, matematiksel güzelliğin fizikteki yeri, tümüyle sorunlu bir kavramdır. Kuramsal fizikçilerin birçoğu, Dirac gibi, bir tür estetik öğreti yaniısı olsalar da, kuramların güzelliği ya da çirkinliği konusunda pek anlaşamazlar. Eğer anlaşırlarsa da, bu genellikle ancak kuramın doğru ya da yanlış olduğu kanıtlandıktan sonradır. Sonuçta bir kuramın, genellikle, matematikse! olarak güzel olduğu İçin doğru kabul edilmek yerine, daha çok deneysel olarak doğru olduğu için ona matematiksel güzellik atfedildiği söylenebilir.
Ne var ki Dirac, böyle sıradan bir görüşü kabul edemezdi. Ona göre, "fizik denklemlerinde matematiksel güzellik olmaması, onlarda bir eksiklik olduğunu, kuramın da düzeltilmesi gereken bir hata içerdiğini gösterir."
Kragh, H. "Paul Dirac: Seeking Beauty" Physics World, Ağustos 2002
Çeviri: Nermin Arık
|
|
|
|
Dirac, bir kuramsal fizikçi olarak çok başarılı olduğu halde, kabul görmeyen ve günümüzde neredeyse unutulmuş olan alışılmadık kuramlar geliştirmeye de çok zaman harcardı. Kendine kuan-tum mekaniği kadar yakın olan bu türden bir kuram, kütleçekim sabitinin zamanla değişmesine dayanan bir kozmolojik kuramdır.
1930'lu yılların ortalarında Dirac, Eddington ve Edward A. Milne'nin "kozmo-fiziksel" görüşlerine ilgi duymaya başladı. Eddington, fizik sabitlerinin boyutsuz kombinasyonlarının önemini vurgulamıştı. Bunlar arasında özellikle ince-yapı sabiti a ile ilgileniyordu; e bîr elektron yükü, h Planck sabiti bolü 2n ve c ışık hızı olmak üzere a= e2/hc~ 1/137'dir, Dirac, boyutsuz sayıların çok önemli olduğu konusunda Eddington ile aynı fikirdeydi; ama 1039 ve karesi olan 1079 düzeyindeki çok büyük sayılara odaklanıyordu.
1937 ve 1938'de yazılmış makalelerde Dirac genellikle ilke olarak şunu ileri sürüyordu: Eğer İki büyük boyutsuz sayı, temel doğa sabitlerinden oluşturulabilirlere, basit bir matematiksel ilişkiyle bağlantılı olmalıdırlar. Büyük sayı varsayımı denen bu varsayımdan yola çıkarak, Newton'un kütleçekim sabiti G'nin zamanla çok yavaş olarak değiştiğini kabul eden yeni bir kozmolojik model oluşturdu. Elektromanyetik ve kütleçekim kuvvetlerini evrenin yaşına (Hubble zamanı) bölerek, G'nin yılda 10" gibi yavaş bir hızla değiştiğini ileri sürdü.
Dirac ve başka bazı fizikçilerin sayısal rastlantılara -George Gamow'un deyişiyle kozmonüme-rolojiye- verdikleri önem, eski Yunan felsefesinde tam sayıların anlamına duyulan metafiziksel inancın bir yansımasıydı. Pisagor kökenli düşünce ekolüne göre, sayısal rastlantılar ve doğadaki
|
düzenlilik gelişigüzel olmayıp, doğa yasalarındaki düzenin çeşitli gösterimleriydi. Pisagor gibi Dirac da evrenin gizemlerinin en sonunda tamsayılarla açıklanabileceğine inanıyordu. Dirac, 1939'da verdiği bir konferansta, evrendeki bütün olayların, 1039 sayısının özellikleriyle eşleştiğini ileri sürdü. "Böylece eski filozofların, tüm doğayla tamsayılar arasında bağlantı kurma hayallerinin gerçekleşmesi mümkün olabilir" diyordu.
Dirac'ın kozmoloji kuramı, çoğu bilimcinin benimsediği deneysel bilim ilkelerinden yoksundu. Kuram 1937'de ilk ortaya çıktığında, Lond-ra'daki Imperial College'de astrofizikçi ve filozof olan Herbert Dingle "sakat bir akılla sarhoş bir hayalin ürünü... sözde bir omurgasız kozmo-mito-loji bilimi" nitelemesiyle ona şiddetle karşı çıkmış, bu saldırı Nature dergisinde hararetli tartışmalara yol açmıştı. Ama Dirac, felsefi tartışmaları engellemek için sesini fazla yükseltmeyerek, bu tür tartışmaları kozmolog meslektaşları Eddington ve Milne'ye bırakmayı yeğledi.
Dirac, yaşamı boyunca , G'nin değiştiğine dayanan, fizikçilerin ve gökbilimcilerin pek desteklemedikleri alışılmış-dışı kuramına bağlı kaldı. Ne var ki, onu kuramın doğru olduğuna ikna eden şey, kısmen, çok güzel olduğunu düşündüğü bir matematiksel çerçevede İfade edilebilmesiydi. Kuramının yöntemsel ve estetik erdemlerini vurgularken deneysel desteklerden yoksun olmasını Önemsemedi. Kurama karşı gelen ölçüm ve tartışmaları kabul etmek istemeyişi de, ona ne denli bağlandığının bir göstergesi. 1980'lerin başlarında yapılan gözlemler, G gerçekten değişiyor olsa bile değişme hızının Dirac'ın kuramının öngördüğünden çok daha yavaş olacağını gösterdi. Ama Dirac yine de kuramının doğru olduğunda ısrarlıydı.
|
|
|
|
|
|
|
|
Ocak 2004 87 BİLİM veTEKNİK
|
|
|
|
|
|
|
|
|
|
|
|
|
|